RedQueen
An Online Algorithm for Smart Broadcasting in Social Networks
Social media is a broadcasting platform
Everybody is a broadcaster
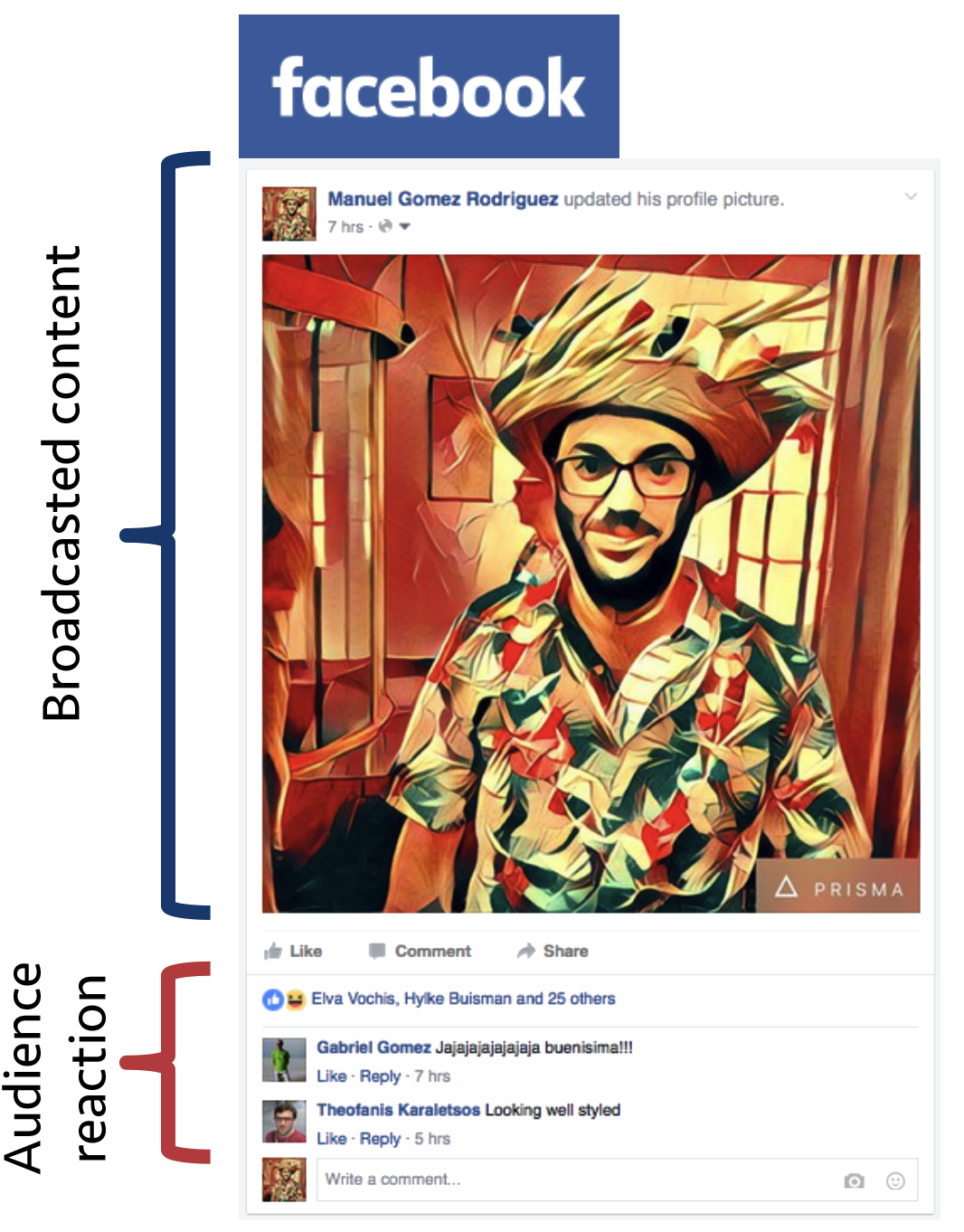
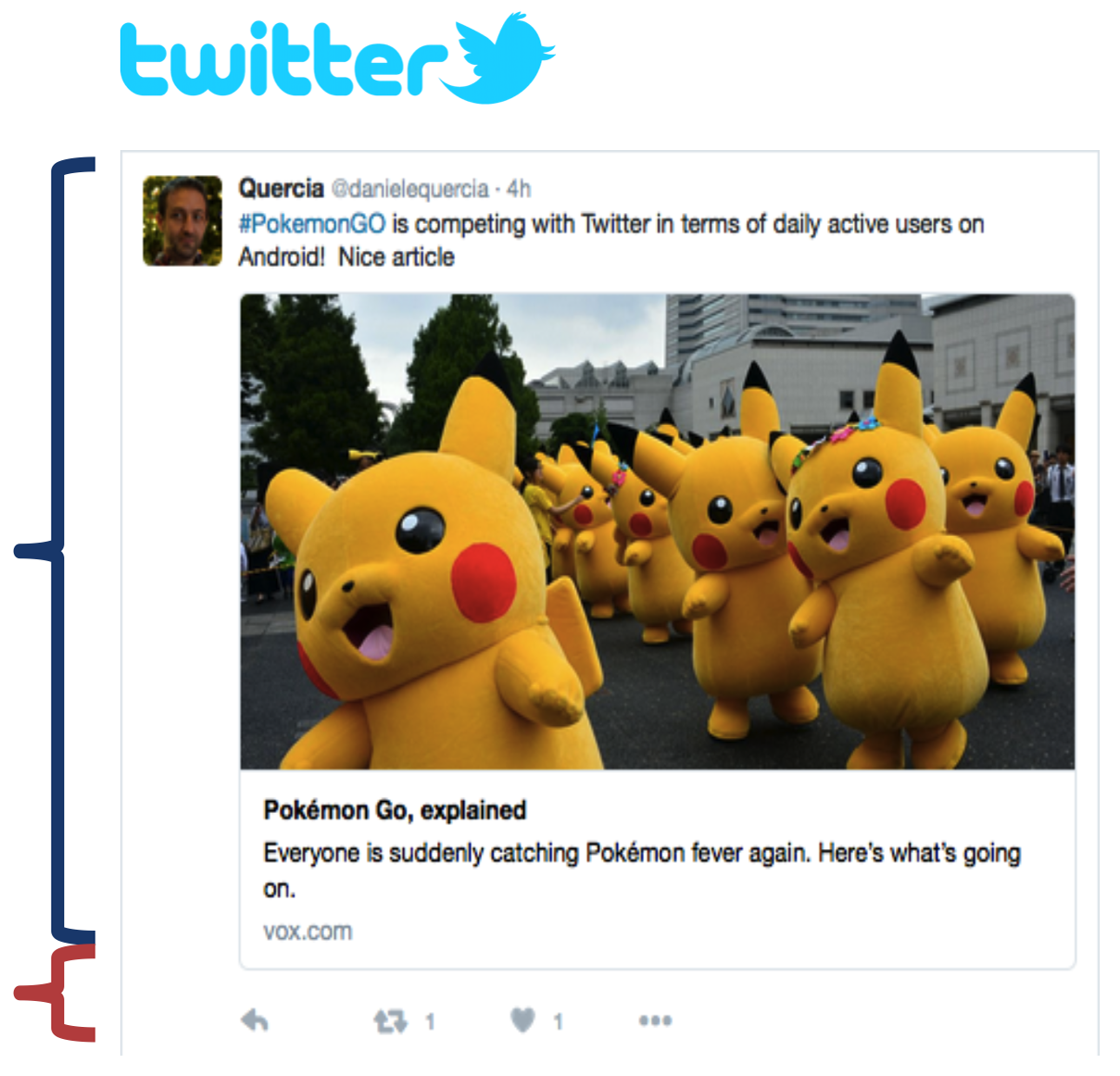
User attention is scarce
Not all posting times are the same.
When-to-post
Problem setup
\( r(t) \): position of the highest ranked post by our broadcaster on the follower's feed.
Dynamics of inverse-chronological rank
$$
r(t+dt) = \left\{
\begin{array}{cl}
& r(t)+1 & {\color{other} \text{Others post}}\\
& 0 & {\color{us} \text{Our broadcaster posts}}\\
& r(t) & \text{No-one posts}
\end{array}
\right.
$$
Posting dynamics using temporal point processes
Other broadcasters can be bursty with time varying rates, which we cannot control.
Posting dynamics using temporal point processes
We would like to control our rate of posting \( u(t) \) to minimize \( r(t) \).
Optimal rate of posting
For a very general class of behavior of other broadcasters, the optimal rate of posting is \( u^{*}(t) = c \times r(t) \).
\( u^{*}(t) \) to when-to-post
Since \( u(t) = 0 \), so we do not need to post at all.
\( u^{*}(t) \) to when-to-post
We take one sample from \( exp(c) \) to determine our next post's time.
\( u^{*}(t) \) to when-to-post
If other broadcasters post in the meanwhile, we may revise our planned posting time.
\( u^{*}(t) \) to when-to-post
However, we may not update our time if we planned to post was earlier than the new sampled time.
\( u^{*}(t) \) to when-to-post
After we post, we start this process all over again.
Results
Average rank
\( 72\% \) average drop in rank, lowered for all users
Demo
Time at top \( \int_{0}^{t} \mathbb{I}(r(\tau) \lt 1)\, d\tau \)
Questions?