Memorize

Introduction

It is well known that repeated and spaced reviews of knowledge is necessary for improving retention. However, it is unclear what is the best schedule for reviewing. Several heuristics have been suggested, but they lack guarantees of optimality. See Lindsey et al, Pashler et al., Metzler-Baddeley et al., Pavlik et al, Reddy et al., etc. In this work, we will describe a way of coming up with an optimal scheduling algorithm which we name Memorize.

Problem setup

Let us consider the problem of learning one knowledge item. We assume that we know how difficult learning the item is. We will formalize these parameters later. These parameters can be estimated from a dataset of learning traces. Depending on the size of the dataset, these parameters can be user-specific, item-specific, or even user-item specific. Our algorithm will determine the time the item is to be reviewed by the learner. The learner will be tested at that time to see if he can recall the item and our algorithm will update our next-reviewing time based on that information, adapting to the user.

The objective of the algorithm is to keep the recall of the item high during the experiment duration \( (0, T] \) while minimizing the total number of reviews that the learner has to do.

Memory models

Before we can start talking about scheduling, we need a model of human memory, which can help us predict how humans forget. There are multiple models of memory which can predict the probability of recall at time \( t \) given the past reviews of the item and its difficulty. See ACT-R, Multiscale Context Model (MCM), Power-law, etc.

⊕ An example of how the probability of recall may change with time. As soon as a review happens, the recall probability jumps to \( 1 \). It rate of decay depends on the forgetting rate \( n(t) \).

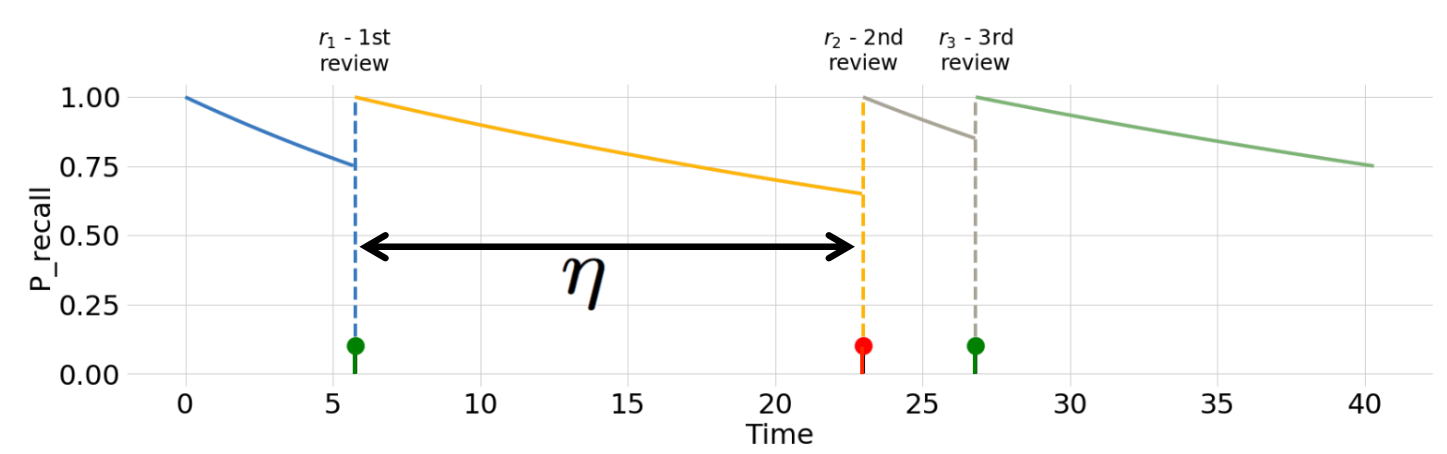
We will assume that the probability of recall follows the analytically simple exponential forgetting curve model. In our paper, we have extended the analysis to more widely accepted power-law forgetting curve model of memory as well.

In the exponential forgetting curve model of memory, we assume that probability of recall \( m(t) \) of the item immediately after a review is \( 1 \). Then, as the name suggests, the probability of recall \( m(t) \) decays exponentially with a forgetting rate \( n(t) \), which depends on the past reviews and the item difficulty: $$ m(t) = e^{-n(t)(t - t_{\text{last review}})} $$ ⊕ The power-law forgetting curve model is \( m(t) = (1 + \omega (t - t_{\text{last review}}))^{-n(t)} \), where \( \omega \) is a parameter we learn from the data. Our estimate of the forgetting rate is adapted to be higher or lower depending on whether the learner managed to recall the item at a review or not: $$ n(t + dt) = \begin{cases} (1 - \alpha) \times n(t) & \text{if item was recalled}\\ (1 + \beta) \times n(t) & \text{if item was forgotten} \end{cases} $$ \( \alpha \) and \( \beta \), as well as the initial difficulty \( n(0) \), are parameters of the model which are derived from the dataset using a variant of Halflife regression.

Methodology

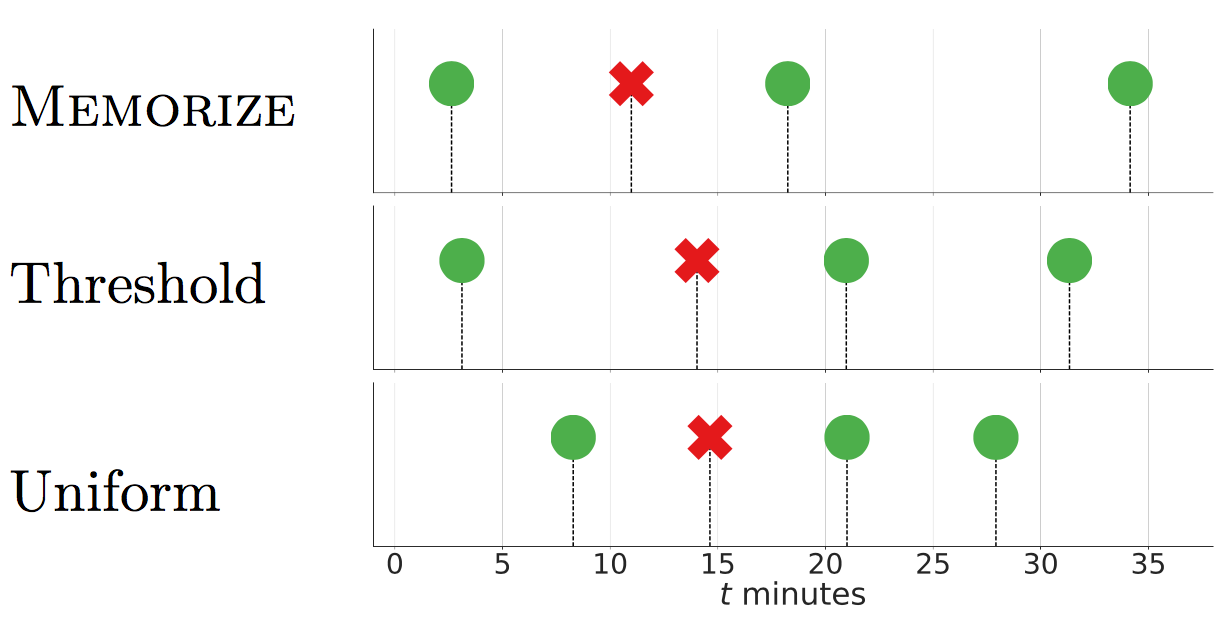
Previous approaches usually directly attempt to produce the optimal time to review either by discretizing time into fixed sized slots (e.g. hours or days) or by using a thresholding based strategy (which schedules a review just when the recall probability falls under a fixed threshold). However, instead of optimizing for the exact time of review, we will aim at uncovering the optimal rate of reviewing.

⊕ The relationship between intensity \( u(t) \) and the number of reviews \( N(t) \). When the intensity is higher, the events happen with a higher rate, or more frequently.

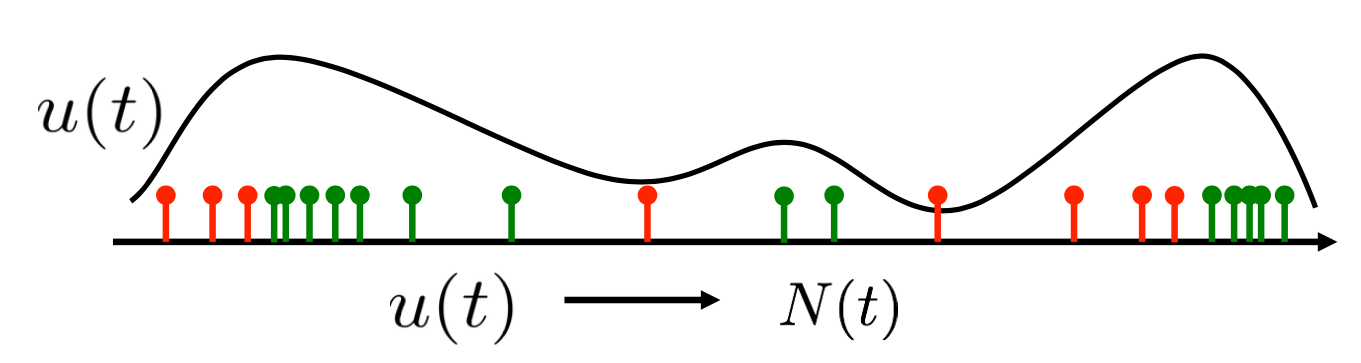
This change will allow us to formulate the discovery of the optimal reviewing schedule as a stochastic control problem. However, before that, we have to choose a loss function which the optimal reviewing schedule ought to minimize.

We choose the following loss function $$ \begin{align} \underset{u(0, T]}{\text{minimize}} & \quad \mathbb{E}_{ \{ \text{reviewing times} \} }\left[ \int_{0}^{T} \left( \,(1 - m(\tau))^2 + \frac{1}{2} q\,u^2(\tau) \right) d\tau \right] \\ \text{subject to} & \quad u(t) \geq 0 \quad \forall t \in (0, T] \end{align} $$ This loss penalizes high probability of forgetting \( (1 - m(t))^2 \) as well as high review rates \( \frac{1}{2} q\,u^2(t) \), with \( q \) acting as a tunable parameter to trade off between these objectives.

We integrate the this loss function over the experiment interval \( (0, T] \) and, since the reviewing times are stochastic, we attempt to find the reviewing rate \( u(t) \) for the item which minimizes the expectation of the integral.

With this choice of the loss function, the optimization problem can be solved analytically by formulating the optimal cost-to-go, deriving a PDE using the Hamilton-Jacobi-Bellman equation and then solving it.

Finally, on solving the PDE, we arrive at the following elegant solution: $$ \overbrace{u(t)}^{\text{reviewing intensity}} = q^{-{1}/{2}}\,\underbrace{(1 - m(t))}_{\text{Prob. of forgetting}} $$

This function states that the rate at which the item must be reviewed (i.e. the urgency of reviewing), should be proportional to how close the learner is to forgetting that item. Hence, the urgency to review increases as the recall rate \( m(t) \) drops. If the user remembers the item perfectly, i.e. \( m(t) = 1 \), the rate at which reviews will happen will be 0, i.e. no reviews will be scheduled. Similarly, if the user has completely forgotten the item, i.e. \( m(t) = 0 \), the learner will see review events with rate \( q^{-{1}/{2}} \) per unit of time.

Note that this is different from scheduling a review after the probability of recall hits a certain threshold. That is a deterministic heuristic policy which attempts to prevent the probability of recall from falling below a threshold. Our policy, on the other hand, is stochastic in nature and is provably optimal for our loss function.

From rate-of-reviewing to next-review-time

Now that we know the rate at which the item should be reviewed, we have to determine when exactly should the next post be made. This can be done easily using thinning of Poisson process because we know what the maximum reviewing intensity is, i.e. \( q^{-{1}/{2}} \).

Evaluation

To evaluate our scheduling, we used the dataset made available at duolingo/halflife-regression. First, we determine how close a given schedule is to Memorize, or any of the baselines, and then we determine what the performance of the people who follow each scheduling strategy most closely, i.e. are in the top 25%-quantile of using that particular strategy by likelihood.

⊕ Example of traces close to various schedules for the same recall pattern (✔, ✕, ✔, ✔). Memorize and Threshold based strategy have similar looking traces, as they both respond to whether the learner got the answers right (next review is further away) or wrong (next review closer). However, while the scheduling by Threshold is a heuristic, the traces generated by Memorize are stochastic and provably optimal. The Uniform scheduler has even spacing between all reviews irrespective of whether the learner was able to recall the item or not.

We found that the empirical forgetting rate for the learners who followed Memorize for our method was much better than for the other baselines.

⊕

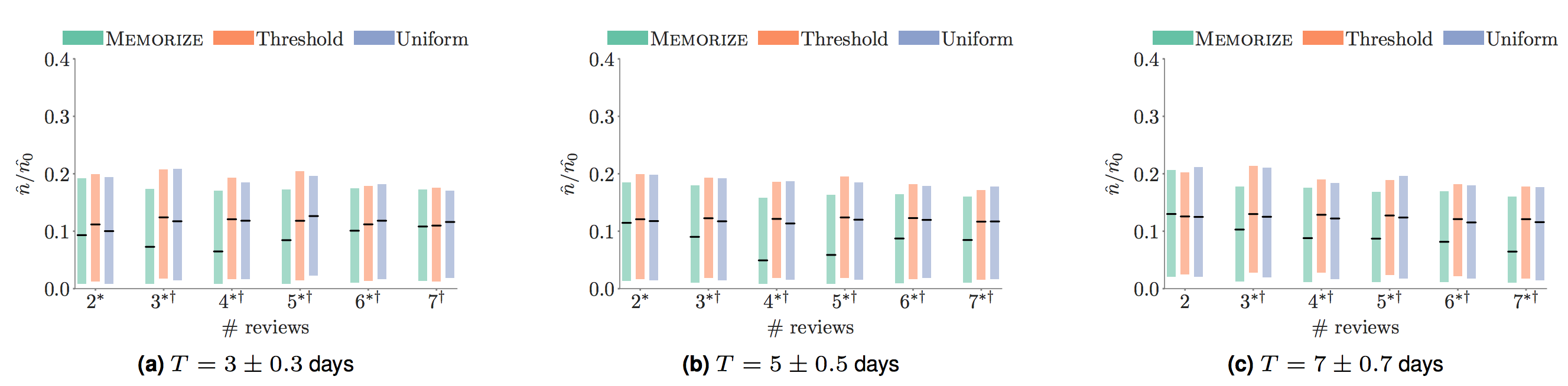
The relative empirical forgetting rate for (item, learners) who follow Memorize is much lower than for other pairs which follow other baselines while controlling for the total duration of study.

More details

Our paper contains a mathematical description of Memorize, and several extensions:

• Extending the one item algorithm to multiple items.
• Using the power-law forgetting curve.
• Proof of optimality of the solution.
• More experiments comparing performance of learners who followed Memorize like scheduling and other schedulers.

Authors

The authors of Memorize are Behzad Tabibian, Utkarsh Upadhyay, Abir De, Ali Zarezade, Bernhard Schölkopf and Manuel Gomez-Rodriguez. The webpage was created by Utkarsh Upadhyay.